Fen Dersleri

Arşimed ve Pascal ın hayatı

ARŞİMET’İN HAYATI : Eski Yunan matematikçi ve fizikçisidir. (Syrakusai M.Ö. 287-ay.y. 212) Genç yaşta öğrenimini tamamlamak ve ünlü bilim adamı Eukleides’ in derslerini izlemek üzere Antik çağın kültür merkezi olan İskenderi‘ ye gitti. Yer kürenin çevresini zamanına göre çok iyi bir yaklaşımla veren Eratusthenes ile tanıştı. Yurduna döndükten sonra kendini tamamıyla ilmi çalışmalara adadı. Matematik, fizik ve astronomi üzerinde çalıştı.
İlk olarak Arşimet daire çevresinin çapına oran olan pi sayısını,daire içine ve dışına çizilmiş düzgün çokgenler yardımıyla yaklaşıklıkla veren bir metot ortaya koydu. Çok büyük sayıları kolaylıkla belirtmeye yarayan bir yöntem bularak Yunan sayı sistemini geliştirdi. Yayların toplama ve çıkarma formüllerini buldu. Koniklerin (elips, parobol,hiperbol) kendi çevresinde dönmesiyle oluşan geometrik şekilleri inceledi. Arşimet ‘in mekanik alanda da başarıları vardır. Sonsuz vidanın hareketli makaranın, palanganın ve dişli çarkın bulucusu olarak tanınır. “Bana bir dayanak noktası gösterin dünyayı yerinden oynatayım” sözü Arşimet’e aittir.
Kurumsal çalışmaları yanında söylenceleşmiş pratik çalışmalarıda vardır. Bunlardan en ünlüsü Syracusa kralı ve dostu Hieron ‘un kendisi için yaptırdığı altın taca başka bir maden karıştırıldığından kuşkulanarak Arşimet ‘ten taç bozulmadan bunu ortaya çıkarmasını istemesiyle ilgilidir. Arşimet bu sorun üstüme düşünür, ancak birşey bulamaz. Bir gün hamamda yıkanırken suyun vücudunun batan bölümünün hacmiyle orantılı bir kuvvetle yukarı doğru ittiğini bulur. Bu yolla tacın saf altından yapılıp yapılmadığını düşünen Arşimet büyük bir sevinçle çrılçıplak olrak sokağa fırlamış ve bağırmıştır: Eureka, Eureka (buldum, buldum )…
Ayrıca Arşimet M.Ö. 215’te Konsal Marcellus komutasındaki Roma ordusuna karşı Syracua kentinin savunmasında yer aldı. Bu savunmada çok uzak mesafelere ok ve taş atan mekanik aletler yaptığı ve kurduğu ayna sistemiyle güneş ışınlarını Roma donanması üzerinde odaklayarak gemileri yaktığı söylenir. Herşeye rağmen Romalılar bir şans eseri Syracusa’ ya girdiler. Marcellus, askerlerine bu büyük adama iyi davranılmasını emretmiştir. Ancak Arşimet ‘I tanımayan bir asker bir problemin çözümüne iyice dalmış olan bilginin kendisine cevap vermemesi üzerine kızarak öldürdü.
Arşimet Prensibi : cisimlerin sıvı ya da gaz ortamlar içerisindeki denge koşullarını açıklayan, fiziğin temel ilkelerinden biridir.
Arşimet’in ortaya koyduğu bu ilkeye göre sıvı ya da gaz ortam içeresinde bulunan bir cismin ağırlığı, kendi hacmine eşit hacimdeki sıvının (gazın) ağırlığı kadar azalır. Eğer cismin yalnız bir bölümü sıvı (gaz) ortam içerisinde bulunursa ağırlığı kadar azalır. Buna göre hacmi V,ağırlığı G, ve yoğunluğu Q olan bir cismin sıvı (gaz)ortam içerisine kalan bölümün hacmi V, sıvının (gazın) yoğunluğuda Q ise cismin sıvı (gaz) ortam içerisindeki ağırlığı G=G-F’ dir. Böylece cismin ağırlığındaki azalmaya neden olan ve sıvı (gaz) tarafından yukarıya doğru etki ettirilen F kuvvetine kaldırma kuvveti denir. Bu kuvvet cismin, sıvı(gaz) içinde kalan bölümün hacmi kadar hacimdeki sıvının ağırlığına eşit olduğundan Arşimet ilkesi matematiksel olarak :
F=VQ-V’Q’=(V-V’)Q=V’Q’ Bağıntılarıyla gösterilir.
Arşimet ilkesinin ilginç sonuçlarından birisi, cismin sıvı ya da gaz ortam içerisinde bulunan bölümün hacmine eşit hacimdeki sıvı ya da gazı, bulundukları kaptan taşırmasıdır. Bu bakımdan kaldırma kuvveti, taşan sıvı ya da gazın ağırlığına eşittir. Bu olay, içinde su bulunan ölçekli bir kaba uygun bir cisim atılarak kolayca gözlenebilir.
PASCAL:(19 Haziran 1623- 19 Ağustos 1662)
Blasie Pascal; Fransız matematikçisi, fizikçisi, felsefecisi ve yazarıdır. Akışkanlar yasalarından biri olan pascalı bulmuştur.
Clermont Vergi Mahkemesi başkanı olan babası iyi bir matematikçi ve bilgili bir kişiydi. Karısının ölümünden 5 yıl sonra ailesiyle birlikte Paris ‘e yerleşti. Fiziğe ve matematiğe duyduğu ilgiden dolayı dönemin tanınmış edebiyat ve bilim adamlarıyla bağlantı kurdu. Küçük yaşta gelişen yetenekleri sayesinde birlikte olduğu çevreye yabancılık çekmedi. Babasıda oğlunun bu yeteneklerini farkedince oğluna ders vermeye başladı.
Henüz çocuk denilecek yaştayken, Eukleides’in ilk 32 teorisini öğrenen, 11 yaşında sesler üstüne bir inceleme yazan (Tratie surles sons (sesler üstüne inceleme)) Blasie Pascal, 12 yaşına gelince kendi kendine geometri öğrendi. Daha sonra sesin hızını ölçen P.Mersone’in (1588-1648) düzenlediği bilginler arası toplantılara katıldı. Pascal 16 yaşında Desan ques‘in 1639’da izdüşümsel geometri kitabından esinlenerek Essai sur les coniques (konikler üstüne deneme) adlı yapıtını yazdı. 1639’da Rouen’da maliye dairesinde önemli bir göreve atanan babasıyla birlikte gitti, onun işlerini kolaylaştırmak amacıyla bir hesap makinesi tasarladı. Jansenusçula bağlandı. Bu arada Toriçelli’nin tüpler içinde sıvıların yükselmesi, havanın ağırlığı vb. üstüne deneylerini yineledi, boşluk konusunda çalışmalar yaptı. 1647’de “Boşlukla İlgili Yeni Deneyler” adlı incelemesini yayımladı. Boşluk incelemesine girişide bu dönemde yazdı.
1647’den sonra kız kardeşi jacquleline ile Paris’e yerleşmiş olan Pascal’ın sağlık durumu iyiden iyiye bozulmuştu. Doktorların önerilerine uyup gezip dolaşmaya, salonlara girip çıkmaya başladı, liberten kişilerle bağlantı kurdu.
1651’de babası ölmüş, kızkardeşiyle Port Royal Manastır’a gitmiştir. Pascal’ın monden yaşamı 1654’te sona ermişti. Çünkü fikirleri değişmişti. 23 Kasım 1654’te şiddetli bir diş ağrısı nedeniyle uykusuz geçen bir gecede sikloit eğrisi üzerinde düşünmeye başlayan Pascal, bunu izleyen sekiz gün içnde sikloite ilişkin önemli buluşlar ve Port Royal’a girişinden sonraki tek bilimsel çalışması “Sikloit Üzerine” (1658) adlı yapıtını yayımladı. Pascal “Hristiyan Dininin Savunması” adlı bir yapıt yayımlamayı düşünüyorken öldü.

Gemilerin Tarihi Gelişimi

Deniz ya da büyük su kütleleri üstünde bir yerden bir yere ulaşmak , yük ve yolculuk için yapılan, yelken ya da yakıt gücüyle çalışan teknedir. İÖ 4000 sonralarında ilkel sallardan daha karmaşık teknelerin yapıldığı Mısır, geminin anayurdu olarak bilinir. Bunlar genelinde kürek ve bir büyük yelken yardımımıyla hareket eden, içi oyulmuş kürekten yapılma teknelerdi. İÖ 150’LERDE Akdeniz’de üstün bir deniz gücü olan Giritlilerin İÖ 700’lerde yerini Fenikeliler aldı. Ancak, Yunan ile Roma döneminde gemilerin kadırga ya da savaş gemisi ve kıç güvertesi kamaralı tekne ya da ticaret gemisi olarak iki belirli türe ayrılırdı.
Ortağçağ başlarında çoğu Akdeniz yük gemilerinin hantal kare yelken yerine üçgen latin yelkenlerini benimsedikleri görülür. Latin donanımı, 7.yüzyıl Müslüman fetihlerinden sonra yaygınlık kazanmıştır. Bu arada Vikingler ya da Kuzey adamları uzak bölgelere akıp yerleştiktikçe İngiltre ve İrlanda’da Danimarkalılar, Fransa ve İtalya’da Normanlar, Rusya’da İskandinavyalılar ya da Varengler olarak tanındılar. Viking gemileri genellikle 21 m uzunluğunda,
4 m genişliğindeydi.
Barutun bulunuşu ve 1350’den sonra gemilerde ilk kez top kullanılması sonucu savaş gemileri ticatet gemilerinden giderek daha çok başkalaştı. 1400’lerde Ege Adaları’na yayılan ve denizcilikte oldukça yeni bir ulus olan Türkler güney tipi geminin yapımını gerçekleştirdiler. Baştaki en büyük olmak üzere üç direkli, Latin yelkeni donanımlı ve kadırgaya oranla daha hafif bir savaş gemisi olan karevela, özellikle Fatih Sultan Mehmet’in bu türden oluşan gemileri karadan Haliç’e indirmesinden sonra Akdeniz’den kuzeye bazı değişimler geçirerek hızla yayıldı.
Karevelanın tüm Avrupa’ya kazandığı yaygınlığıa karşı (1492’de Kristof Klomb’un üç direkli tam aramalı Santa Mariasına eşlik eden Nina ve Pinta gibi; ya da 14976-1499 arasında Hindistan’a giden deniz yolunu açan Vasco de Gama’nın filosundaki gemiler)askeri alanda gelişik kadırga, 1538’de Barboros’un Preveze’de Haçlı donanmasını ywenmesiyle denizlerde sürdüğü üstünlüğün doruğunu erişti.ve 1571’de ispanyol ile İtalyanların İnebahtın’da Türkleri yenmelerinden sonra önemini yitirmiştir.
19.yüzyıl ortalarında buharın ortaya çıkması sonucu dünya deniz kuvvetlerinde yelken hızla geriledi. Ticaret filosunda ise yelkenlinin altın çağı buharın gelişiyle ansızın sona ermedi. Savaş gemileri tersine, yelkenli ticaret gemileri 1838’de buhar gücü Avrupa’dan Atlas okyanusunun karşı yakasına ulkaştıktan sonraki 30 yıl içinde görkemli doruklarına ulaştılar. 1869’da Süveyş Kanalı’nın açılmasıyla yelkenli gemiler için,ağır bir darbe oldu. Dört köşe seren yelkenli kabasortalar Kızıldeniz’in kararsız rüzgarları karşısında güçlükle yol alamamışlardır.
1903’te Hazar Denizi’nde küçük bir yük gemisine dizel motoru denendi. Düşük değerli yakıt yaktığı için kullanımı ucuz bir iç yakıumlı makine olarak kısa bir süre kömür tozu tükettikten sonra mazot yakmasında karar kılındı.1912’de Danimarka yapımı Selandia açık denize çıkmaya elverişli ilk dizel motorlu gemidir. Mazotlu dizel motorların yapımından sonra petrolün genmi yakıtı olarak değeri arttı. 1980’li yıllarda yük ve yolcu gemileri, ticaret ve gezi istemlerini karşılamak amacıyla,gerek çizim,gerekse kullanım açısından köklü değişimlere uğradılar.

Sıvılar Cisimlere Kaldırma Kuvveti Uygular (Konu Anlatımı)

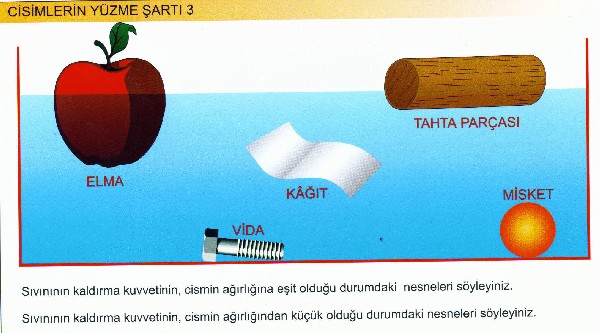
Deniz, göl ve akarsularda büyüklükleri ve cinsleri birbirinden farklı olan pek çok cisim görürüz. Bu cisimlerin kimi su yüzeyinde yüzer, kimi su içerisinde farklı derinliklere iner, kimi de dibe batar. Cisimlerin sudaki konumlarını belirleyen etkinin cevabını 2200 yıl önce Archimedes (Arşimet) vermiştir. Rivayete göre Archimedes bir gün banyo yapmak için su dolu bir küvete girer. Küvetin kenarlarından taşan suyu görünce, bu suyun ağırlığı ile kendi vücut hacminin suda kalan kısmı arasında bir ilişki olabileceğini düşünür ve cisimlerin bir sıvıda yüzmesi ya da batmasıyla ilgili bir sonuca ulaşır.

Havada uçan balonlara, uçurtmalara, kuşlara ve uçaklara olduğu gibi suda yüzen balıklara, gemilere ve kayıklara da Dünya'nın
merkezine doğru (aşağı yönde) şekildeki gibi bir çekim kuvvetinin etki eder. Dolayısıyla cismin, sıvadaki ağırlığı havadaki ağırlığından, sıvının uyguladığı kaldırma kuvveti kadar azalmış olur. Sıvı içerisine bırakılan herhangi bir cisme görüldüğü gibi değişik yönlerde ve farklı büyüklüklerde itme kuvvetleri etki eder.

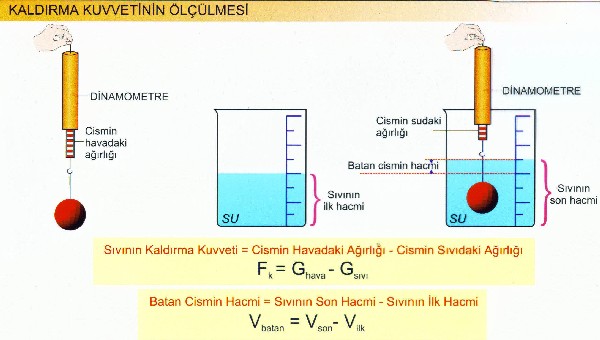
Eğer yukarıdaki deneyi etil alkol ile yapmış olsa idik V_batan yani cismin suya girince değiştirdiği hacim miktarı , sudaki ile aynı olacaktı. Fakat kaldırma kuvveti sadece V_batan a bağlı değildir . İçine girdiği sıvının yoğunluğuna da bağlıdır.

d_su > d_{etil alkol}  suda daha fazla bir kaldırma kuvveti söz konusudur.

"Kaldırma kuvveti, cismin sıvıya batan kısmın hacmi yanında batırıldığı sıvının yoğunluğuna da bağlıdır."

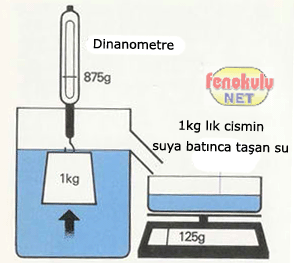
Yukarıdaki şekilde 1 kg lık cisim suya girince batan kısım kadar su taşırdı. Taşırdığı su miktarı 125 gr dır. Suyun 1 kg lık cisme uyguladığı kaldırma kuvveti siyah okun yönünde kuvvet ise 125 gr lık bir kuvvet olmuştur. Cismin ağırlığı ise 1000gr-125gr=875gr dır.

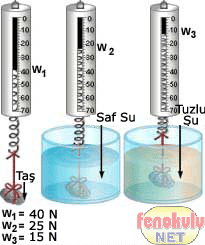
Yukarıdaki şekilde Taş havada dinamometre ile ölçülüyor ve 40 N bulunuyor.

2. Durumda suyun içine batırılarak ölçüm yapılıyor ve Dinamometredeki değer 25 N okunuyor. Buradan suyun taşa uyguladığı kuvvet 40-25=15 N olarak bulunabilir.

3. Duruda cisim tuzlu suyun içine batırılarak ölçüm yapılıyor.Dinamometredeki değer 15 N okunuyor. Buradan suyun taşa uyguladığı kuvvet 40-15=25 N olarak bulunabilir.

Buradan tuzlu suyun cisimlere daha fazla kaldırma kuvveti uyguladığı görülebilir. Tuz , suyun yoğunluğunu arttırarak kaldırma kuvvetini arttırmıştır. Denizde daha kolay yüzülmesinin sebebi suyun daha fazla kaldırma kuvveti uygulamasıdır.

Örnek Uygulamalar 1

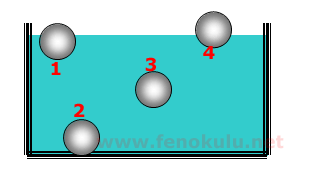
Şekildeki farklı maddelerden yapılmış, eşit hacimli 1.2.3.4. katı cisimleri şekilde ki gibi suyun içinde dengededir.
a)Suyun bu cisimlere uyguladığı kaldırma kuvvetlerini karşılaştırınız.

Fk=Cisme Uygulanan Kaldırma Kuvveti

Vb=Cismin batan kısmının Hacmi

ds=Suyun veya sıvının yoğunluğu
Fk=Vb*ds*g dir
Bu durumda g ve ds yı tüm cisimler için aynı değeri ifade ettiği için ihmal edebiliriz. Vb kısmı büyük olan cisimlerin Fk larıda büyüktür.
2. ve 3. cisimlerin su içindeki hacimleri eşit olduğu için Fk2=Fk3 dir. ve Fk1 ve Fk4 ten büyük değer alırlar.
Dolayısı ile Fk2=Fk3> Fk1> Fk4 dür.

b)Hangi cisimlerin kaldırma kuvveti ağırlığına eşit olur?
Yüzen ve askıda kalan her cismin ağırlığı kaldırma kuvvetine eşittir.
Buradan G1= Fk1 , G3= Fk3 , G4= Fk4 fakat G2>Fk2 dir.

c)Cisimleri yoğunluklarına göre nasıl sıralarız?
Cisimler yoğunluklarına göre sıralarken az yoğun olanın sürekli çok yoğun olanın üstüne çıktığını bilmek gereklidir. Buradan hareketle d2>d3>d1>d4 diyebiliriz.
 

Örnek Uygulamalar 2

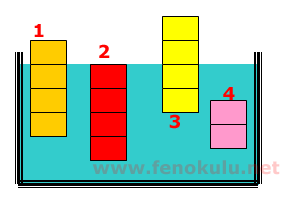
Eşit bölmeli şekildeki 1,2,3,4 numaralı cisimler dengededir.
a)Hangi cisimlere etkiyen kaldırma kuvvetleri eşittir?
Burada yine Fk=Vb*ds*g dir
Bu durumda g ve ds yı tüm cisimler için aynı değeri ifade ettiği için ihmal edebiliriz. Vb kısmı büyük olan cisimlerin Fk larıda büyüktür.
1. cisim Fk1=3V
2. cisim Fk2=4V
3. cisim Fk3=2V
4. cisim Fk4=2V dir dolayısı ile Fk3= Fk4 diyebiliriz.

b)Çözeltiye tuz katılırsa cisimlere uygulanan kaldırma kuvveti nasıl değişir?
Hiçbirinin kaldırma Kuvveti değişmez çünkü tuz katınca suyun yoğunluğu artar. Fakat aynı oranda cisimlerin suya batan kısımlarının hacimleri azalır. Buda Fk=Vb*ds*g dir eşitliğinde bir değişime sebep olmaz. Dolayısı ile yine her cisme uygulanan kaldırma kuvveti tuz katılmadan önceki değeri alır ve değişmez iken suya bata kısımların hacimleri azalıp suyun yoğunluğu artar.

Örnek Uygulamalar 3

Aşağıdaki şekilde havası boşaltılmış fanusta farklı hacimlerdeki iki cisim şekildeki gibi dengededir. Şekildeki havası boşaltılmış fanusa hava verildiğinde son durum ne olur?

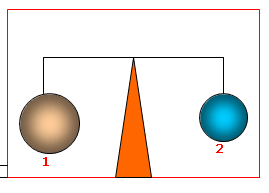
Havasız ortamda sistemin dengede kalması 1. ve 2. cisimlerin ağırlıklarının eşit olduğu anlamına gelir. Fanusa hava verildiğinde hava 1. ve 2. cisimlere kaldırma kuvveti uygular. Hava tarafından hacmi büyük olan 1. cisme daha fazla kaldırma kuvveti uygulanır.. Bunun sebebi aynı kütleye sahip olan iki cisimden 1. sinin hacminin büyük olması nedeni ile daha düşük yoğunluğa sahip olmasıdır. Dolayısı ile Fanusa hava verildiğinde sistem aşağıdaki şekli alır.






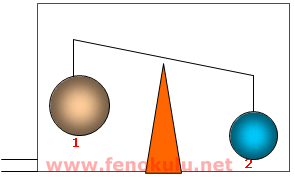
Örnek Uygulamalar 4
 

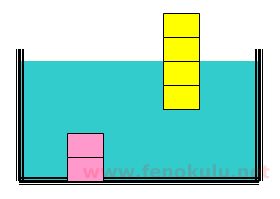
Yukarıdaki şekilde saf su bulunan kaptaki sıvı içine tuz katarsak kapta bulunan cisimlerin son durumları için ne söyleyebiliriz.

 

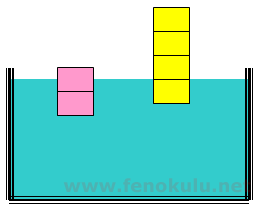
Bir sıvıya tuz katılması o sıvının yoğunluğunu arttırır. Bunun sebebi tuz moleküllerinin su molekülleri içindeki boşluklara dağılarak ağırlığını arttırdığı orandan daha az hacmini arttırmasıdır. Sıvının yoğunlunun artması Fk=Vb*ds*g de ds yi arttırır. Dolayısı ile cisimlere sıvının uyguladığı kaldırma kuvveti artar. Son durumda sıvı içindeki cisimlerin aşağıdaki gibi olması beklenebilir.

Örnek Uygulamalar 5



Şekildeki uçan balonu havaya bıraktığımızda balonumuzun başına neler gelir?



Atmosferde yukarı doğru çıkıldıkça açık hava basıncı azalır. Balonun içindeki basınç ile açık hava basıncı arasındaki denge Balonun içindeki basınç lehine bozulduğu için balonun hacmi artar. Belli bir yükseklikten sonra balonun plastiği bu hacim genişlemesine dayanamayarak patlar. Kafanıza gökten patlak balon düşerse hiç şaşırmayın.

Örnek Uygulamalar 6


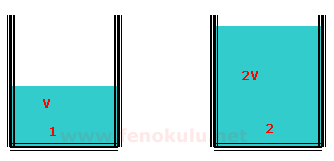
Şekildeki 1 numaralı kapta V hacminde sıvı vardır. Bu sıvının yoğunluğu (Özkütlesi) d dir. Bu kaba aynı sıvıdan V hacminde ilave edildiğinde sıvının son durumda ki yoğunluğu (Özkütlesi) ne olur?


Bir cismin kütlesi arttığı zaman aynı oranda hacmide artar. Bu da o cismin yoğunluğu (Özkütlesi) nu değiştirmez. Birinci durumda d=m/V ise ikinci durumda d=2m/2V dir yine bu iki değer sadeleştirmeler ile aynı değer olan d=m/V yi alır. Tüm okyanusun yoğunluğu ile bu okyanustan alınan bir damla suyun yoğunluğu aynıdır. Tonlarca ağırlığındaki bir kaya parçasının yoğunluğu ile bu kaya parçasından alınan mercimek büyüklüğündeki 2 gr katanın yoğunluğu her yerinde aynı özelliği taşıdığı taktirde aynıdır.

Örnek Uygulamalar 7

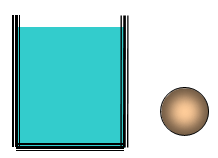
Şekildeki yuvarlak cismi yandaki kapta bulunan sıvının içine attığımız taktirde bu sıvı bu cisme bir kaldırma kuvveti Fk uygular. Bu kaldırma kuvvetini nasıl hesaplayabiliriz?






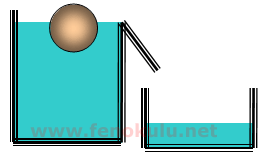
Bir cisme uygulanan kaldırma kuvveti Fk yer değiştiren veya taşan sıvının ağırlığına eşittir. Eğer biz yukarıdaki gibi bir sitem kurar ve taşan veya yer değiştiren sıvının ağırlığını hesaplayabilirsek kap içindeki sıvının cisme uyguladığı kaldırma kuvvetini de bulmuş oluruz.


Örnek Uygulamalar 8



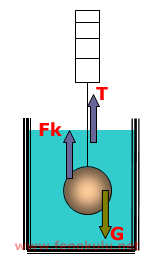
Şekildeki sistem dengede olduğuna göre dinamometre de okunan değer neye eşittir?

Burada 3 adet kuvvet söz konusudur. Bunlar cismin ağırlığı, sıvının kaldırma kuvveti ve dinamometrenin ölçtüğü değerdir. Cismin ağırlığı aşağı doğru, sıvının kaldırma kuvveti ve dinamometrenin ölçtüğü değer ise yukarı doğrudur. Sistem dengede olduğuna göre
Cismin ağırlığı =sıvının kaldırma kuvveti + dinamometrenin ölçtüğü değer
dinamometrenin ölçtüğü değer = Cismin ağırlığı - sıvının kaldırma kuvveti dir.
 

Fatih Akyüz tarafından hazırlanmıştır.